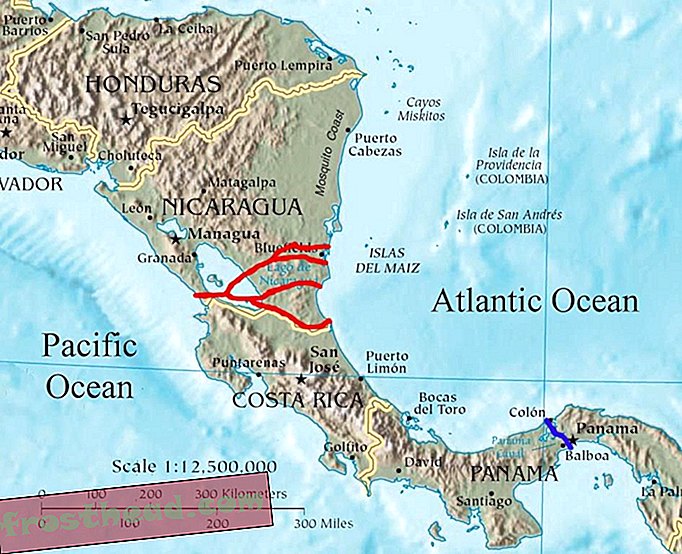
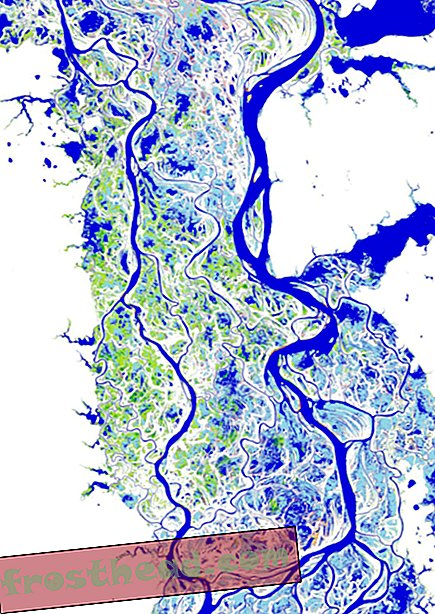
Questa struttura di origami, chiamata "Cicli verdi", di Erik Demaine e suo padre Martin ha richiesto una settimana di improvvisazione per essere assemblata. Credito: Renwick Gallery
Contenuto relativo
- The Romance of Fermat's Last Theorem
La forma di un Pringle, matematicamente parlando, è chiamata paraboloide iperbolico. Gli artisti hanno piegato la carta in questa forma per anni. La svolta? I paraboloidi iperbolici non dovrebbero esistere negli origami: è impossibile realizzare una tale forma 3D usando solo le pieghe pressate sulla carta a mano.
Secondo questa logica, anche alcune delle opere di Erik Demaine non dovrebbero esistere.
Demaine, il principale teorico computazionale dell'origami, ha creato una serie di sculture piegando quadrati concentrici in pezzi quadrati di carta, alternando montagna e valle e piegando le diagonali. Con ogni scultura, la carta si apre in una forma a sella chiamata paraboloide iperbolico e rimane lì. Le sue pieghe a fisarmonica sono belle da vedere, ma Demaine, professore di informatica al MIT, non è sicuro di come funzioni.

Una struttura di carta con più paraboloidi iperbolici. Credito: Erik Demaine
Una volta piegata la carta, l'intera struttura si deposita in una forma naturale. "La fisica trova quell'equilibrio", dice Demaine. Ma i meccanismi della forma simile a Pringle sono ancora poco compresi. Demaine sostiene che ci devono essere piccole pieghe nella carta invisibili ad occhio nudo, poiché le pieghe fatte a mano da sole non possono spiegare la forma finale.
Cercare di risolvere questo mistero significa sposare scultura e matematica.
"Abbiamo riscontrato un problema di matematica che ispira nuova arte e un problema di arte che ispira nuova matematica", afferma Demaine. L'artista 31enne crea le sue sculture di origami con suo padre Martin.
Il prodotto finale, "Green Cycles" (nella foto in alto), è stato creato utilizzando due diversi fogli colorati di carta per acquerello Mi-Teintes di fabbricazione francese, uniti tra loro. Usando un brunitore a sfera, che è essenzialmente una penna a sfera senza inchiostro, i Demaines hanno spinto il foglio a due strati in anelli di cerchi concentrici incisi in un modello di legno. La carta viene segnata lungo le pieghe circolari e tagliata a forma di ciambella, prima che balzi in una forma tridimensionale. L'artista crea alcuni di questi modelli e li unisce in una scultura di carta intrecciata. Il giovane Demaine afferma che la parte più difficile è l'assemblaggio, che richiede fino a una settimana, perché non possono prevedere se le forme risultanti si torcono l'una attorno all'altra per creare un pezzo solido, esteticamente gradevole.
"Li facciamo incastrare, lasciar andare e lasciarli rilassare, a volte dall'oggi al domani, se pensiamo di avere una scultura candidata", dice. Se la struttura si abbassa o cade a pezzi, la coppia riprova.

"Natural Cycles" di Erik e Martin Demaine
Le istruzioni scritte per la piegatura della carta apparvero per la prima volta nel 1797 in Giappone. Akisato Rito ha pubblicato un libro, Sembazuru Orikata, con lezioni per 1.000 gru di carta. Nel 1845 Adachi Kazuyuki pubblicò una raccolta di istruzioni più completa. Alla fine del 1800, gli asili di tutta Europa iniziarono a piegare i quadrati colorati in classe.
Il concetto era semplice: niente forbici, niente colla, niente nastri: solo agili dita che piegavano e torcevano la carta in forme nuove. Origami divenne una forma d'arte moderna negli anni '50, quando Akira Yoshizawa, un artista giapponese, unì la meccanica del mestiere con l'estetica della scultura. Ha creato oltre 50.000 modelli di carta, non vendendone mai uno. Da allora, le figure umane e animali rugose realistiche dell'artista Eric Joisel sono apparse in mostra al Louvre e le dettagliate composizioni dell'artista fisico Robert Lang sono state esposte al Museum of Modern Art.
Ma piegare la carta non solo crea qualcosa in cui possiamo ooh e aah. Svolge anche un ruolo nel rispondere a domande di vecchia data in matematica, come il problema del tipo "taglia e taglia".
Il primo record noto del problema è apparso nel 1721 in un libro giapponese di rompicapo, uno dei quali ha chiesto al lettore di piegare un pezzo di carta rettangolare piatto e fare solo un taglio dritto per produrre una cresta giapponese chiamata sangaibisi, che si traduce in " rombi tripli. ”L'autore ha offerto una soluzione attraverso un diagramma, ma il problema è rimasto una questione aperta per secoli - quante forme sono possibili? - fino a quando Demaine non l'ha risolto.
A quanto pare, è possibile qualsiasi forma: cigni, cavalli, stelle a cinque punte. Tutto ciò che serve è un progetto geometrico, una guida per piegare qui e piegare lì.

"Hugging Circles" di Erik e Martin Demaine
L'uso di tali progetti ha aggiunto complessità agli origami. Negli anni '60, i diagrammi pieghevoli prevedevano da 20 a 30 passaggi. Ora, un modello potrebbe richiedere da 200 a 300 passaggi dall'inizio alla fine. È molto ripiegabile per un singolo pezzo di carta. Ma il trucco sta usando carta super sottile con fibre lunghe, che gli danno la forza per resistere a tutte le operazioni di trazione e trazione.
I programmi per computer si sono solo aggiunti al divertimento. TreeMaker, un programma software gratuito creato dall'artista Robert Lang, prende il disegno generato dagli utenti e sfoggia modelli che possono essere stampati e piegati per creare le forme. Origamizer consente agli utenti di progettare un modello 3D e alterare i suoi motivi di piega sullo schermo, esplorando forme e forme diverse.
Con l'aiuto del software per computer, origami si è espanso oltre il mondo dell'arte. Scienziati e ingegneri hanno trovato applicazioni pratiche per la piegatura della carta. Le case automobilistiche, ad esempio, usano la matematica degli origami per calcolare un modello di piega per piegare gli airbag in forme appiattite. Demaine afferma che le strutture di origami potrebbero influenzare la nanoproduzione, stimolando la creazione di chip con intel piatti che possono scaturire in forme 3D. Lo scorso anno ha anche incontrato membri del National Institutes of Health per discutere di come il velivolo potesse aiutare a progettare proteine sintetiche per combattere i virus.
Il collegamento tra matematica e arte comporta tuttavia alcuni rischi professionali.
"Alcuni tagli di carta all'anno", dice Demaine.
Tre opere del team padre-figlio sono esposte in “4o Under 40: Craft Futures”, una mostra alla Smithwickian's Renwick Gallery fino al 3 febbraio 2013.