Glen Whitney si trova in un punto sulla superficie della Terra, latitudine nord 40.742087, longitudine ovest 73.988242, che si trova vicino al centro di Madison Square Park, a New York City. Alle sue spalle si trova il più nuovo museo della città, il Museum of Mathematics, che Whitney, un ex commerciante di Wall Street, ha fondato e ora dirige come direttore esecutivo. Si trova di fronte a uno dei monumenti di New York, il Flatiron Building, che ha preso il nome perché la sua forma a cuneo ha ricordato alla gente un ferro da stiro. Whitney osserva che da questa prospettiva non si può dire che l'edificio, seguendo la forma del suo blocco, sia in realtà un triangolo rettangolo - una forma che sarebbe inutile per stirare i vestiti - sebbene i modelli venduti nei negozi di souvenir lo rappresentino in forma idealizzata come un isoscele, con angoli uguali alla base. La gente vuole vedere le cose come simmetriche, riflette. Indica la stretta prua dell'edificio, il cui contorno corrisponde all'angolo acuto in cui Broadway attraversa la Fifth Avenue.
Da questa storia
[×] CHIUDI
Un ex "gestore dell'algoritmo" degli hedge fund, Glen Whitney ha derivato la formula per il nuovo Museum of Mathematics. (Jordan Hollender) 
Il fisico Steven Koonin mira a risolvere i problemi del mondo reale come il rumore in eccesso e i tempi di risposta alle emergenze lenti. (Jordan Hollender) 
Man mano che il mondo diventa sempre più urbano, il fisico Geoffrey West sostiene di studiare, piuttosto che di stigmatizzare, le baraccopoli urbane. (Dan Burn-Forti / Contour di Getty Images) 
Lo studio sistematico delle città risale almeno allo storico greco Erodoto. (Illustrazione di Traci Daberko) 
Galleria fotografica
"La traversa qui è la 23a strada", dice Whitney, "e se si misura l'angolo nel punto dell'edificio, è vicino a 23 gradi, che risulta essere approssimativamente l'angolo di inclinazione dell'asse di rotazione terrestre."
"È straordinario", gli viene detto.
"Non proprio. È una coincidenza. ”Aggiunge che, due volte all'anno, alcune settimane su entrambi i lati del solstizio d'estate, il sole al tramonto splende direttamente lungo le file delle strade numerate di Manhattan, un fenomeno a volte chiamato“ Manhattanhenge ”. Quelle date particolari non lo fanno hanno anche un significato speciale, tranne che come ulteriore esempio di come i mattoni e le pietre della città illustrino i principi del prodotto più alto dell'intelletto umano, che è la matematica.
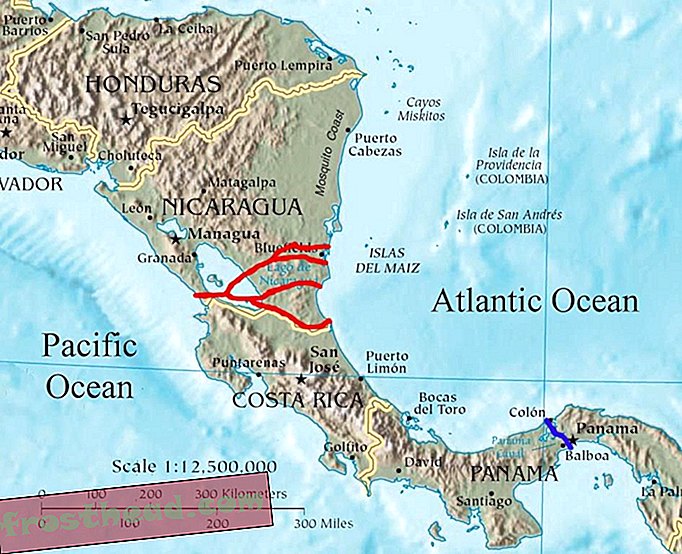
Le città sono particolari: non confonderesti mai una favela a Rio de Janeiro per il centro di Los Angeles. Sono modellati dalle loro storie e incidenti di geografia e clima. Quindi le strade “est-ovest” di Midtown Manhattan corrono effettivamente nord-ovest-sud-est, per incontrare i fiumi Hudson ed East a circa 90 gradi, mentre a Chicago la griglia stradale si allinea strettamente con il nord vero, mentre le città medievali come Londra non lo fanno hanno le griglie ad angolo retto. Ma le città sono anche, a un livello profondo, universali: i prodotti di principi sociali, economici e fisici che trascendono lo spazio e il tempo. Una nuova scienza - così nuova da non avere un proprio diario, o persino un nome concordato - sta esplorando queste leggi. Lo chiameremo "urbanismo quantitativo". È uno sforzo per ridurre a formule matematiche la natura caotica, esuberante, stravagante di una delle invenzioni più antiche e importanti dell'umanità, la città.
Lo studio sistematico delle città risale almeno allo storico greco Erodoto. All'inizio del XX secolo, emersero discipline scientifiche su aspetti specifici dello sviluppo urbano: teoria della suddivisione in zone, sanità pubblica e servizi igienico-sanitari, ingegneria del traffico e del traffico. Negli anni '60, le scrittrici di pianificazione urbana Jane Jacobs e William H. Whyte usarono New York come laboratorio per studiare la vita di strada dei quartieri, i percorsi pedonali dei pedoni di Midtown, il modo in cui le persone si radunavano e sedevano in spazi aperti. Ma i loro giudizi erano generalmente estetici e intuitivi (sebbene Whyte, fotografando la piazza del Seagram Building, derivasse la formula del sedile del pantalone per lo spazio della panchina negli spazi pubblici: un piede lineare per 30 piedi quadrati di spazio aperto). "Avevano idee affascinanti", afferma Luís Bettencourt, ricercatore presso l'Istituto Santa Fe, un gruppo di esperti meglio noto per i suoi contributi alla fisica teorica, "ma dov'è la scienza? Qual è la base empirica per decidere quale tipo di città vogliamo? ”Bettencourt, un fisico, pratica una disciplina che condivide una profonda affinità con l'urbanistica quantitativa. Entrambi richiedono la comprensione di interazioni complesse tra un gran numero di entità: i 20 milioni di persone nell'area metropolitana di New York o le innumerevoli particelle subatomiche in una reazione nucleare.
La nascita di questo nuovo campo può essere datata al 2003, quando i ricercatori della SFI hanno convocato un seminario su come "modellare" - nel senso scientifico della riduzione alle equazioni - aspetti della società umana. Uno dei capi era Geoffrey West, che sfoggia una barba grigia ben rifinita e conserva una traccia dell'accento del suo nativo Somerset. Era anche un fisico teorico, ma si era allontanato dalla biologia, esplorando come le proprietà degli organismi si relazionano alla loro massa. Un elefante non è solo una versione più grande di un topo, ma molte delle sue caratteristiche misurabili, come il metabolismo e la durata della vita, sono regolate da leggi matematiche che si applicano su e giù per la scala delle dimensioni. Più grande è l'animale, più lungo ma più lento vive: una frequenza cardiaca del mouse è di circa 500 battiti al minuto; il polso di un elefante è 28. Se tracciassi quei punti su un grafico logaritmico, confrontando le dimensioni con il polso, ogni mammifero cadrebbe sulla stessa linea o vicino. West ha suggerito che gli stessi principi potrebbero essere all'opera nelle istituzioni umane. Dal retro della stanza, Bettencourt (allora al Los Alamos National Laboratory) e José Lobo, un economista dell'Arizona State University (che si era laureato in fisica come studente universitario), entrarono in contatto con il motto dei fisici fin da Galileo: "Perché don ' otteniamo i dati per testarli? ”
Da quell'incontro è emersa una collaborazione che ha prodotto il seminario sul campo: "Crescita, innovazione, ridimensionamento e ritmo di vita nelle città". In sei pagine piene di equazioni e grafici, West, Lobo e Bettencourt, insieme a due i ricercatori dell'Università di Tecnologia di Dresda hanno elaborato una teoria su come le città variano in base alle dimensioni. "Quello che la gente fa nelle città - crearsi ricchezza o uccidersi a vicenda - mostra una relazione con le dimensioni della città, che non è legata solo a un'era o nazione", afferma Lobo. La relazione è catturata da un'equazione in cui un dato parametro - occupazione, diciamo - varia in modo esponenziale con la popolazione. In alcuni casi, l'esponente è 1, il che significa che tutto ciò che viene misurato aumenta in modo lineare, allo stesso ritmo della popolazione. L'acqua domestica o l'uso elettrico, ad esempio, mostra questo schema; man mano che la città cresce, i suoi abitanti non usano più i loro elettrodomestici. Alcuni esponenti sono maggiori di 1, una relazione descritta come "ridimensionamento superlineare". La maggior parte delle misure di attività economica rientrano in questa categoria; tra i massimi esponenti gli studiosi trovati erano per "lavoro privato [ricerca e sviluppo]", 1, 34; "Nuovi brevetti", 1, 27; e prodotto interno lordo, compreso tra 1, 13 e 1, 26. Se la popolazione di una città raddoppia nel tempo, o confrontando una grande città con due città per metà delle dimensioni, il prodotto interno lordo è più del doppio. Ogni individuo diventa, in media, il 15 percento più produttivo. Bettencourt descrive l'effetto come "leggermente magico", sebbene lui e i suoi colleghi stiano cominciando a capire le sinergie che lo rendono possibile. La vicinanza fisica promuove la collaborazione e l'innovazione, che è uno dei motivi per cui il nuovo CEO di Yahoo ha recentemente invertito la politica della società di lasciare che quasi chiunque lavori da casa. I fratelli Wright potevano costruire da soli le loro prime macchine volanti in un garage, ma non è possibile progettare un aereo di linea in quel modo.
Sfortunatamente, anche i nuovi casi di AIDS si ridimensionano in modo superlineare, a 1, 23, così come i reati gravi, 1, 16. Infine, alcune misure mostrano un esponente inferiore a 1, il che significa che aumentano più lentamente della popolazione. Si tratta in genere di misure di infrastruttura, caratterizzate da economie di scala che risultano dall'aumento delle dimensioni e della densità. New York non ha bisogno di quattro volte più stazioni di benzina di Houston, per esempio; le stazioni di servizio si attestano a 0, 77; superficie totale delle strade, 0.83; e lunghezza totale del cablaggio nella rete elettrica, 0, 87.
Sorprendentemente, questo fenomeno si applica a città di tutto il mondo, di dimensioni diverse, indipendentemente dalla loro storia, cultura o geografia particolari. Mumbai è diversa da Shanghai è diversa da Houston, ovviamente, ma in relazione al proprio passato e ad altre città in India, Cina o Stati Uniti, seguono queste leggi. "Dammi le dimensioni di una città negli Stati Uniti e posso dirti quante polizie ha, quanti brevetti, quanti casi di AIDS", dice West, "proprio come puoi calcolare la durata di vita di un mammifero dalla sua massa corporea."
Un'implicazione è che, come l'elefante e il topo, "le grandi città non sono solo piccole città più grandi", afferma Michael Batty, che gestisce il Center for Advanced Spatial Analysis presso l'University College di Londra. "Se pensi alle città in termini di potenziali interazioni [tra individui], man mano che aumentano, ottieni maggiori opportunità per questo, il che equivale a un cambiamento qualitativo." Considera la Borsa di New York come un microcosmo di metropoli. Nei suoi primi anni, gli investitori erano pochi e le negoziazioni sporadiche, dice Whitney. Quindi erano necessari "specialisti", intermediari che tenevano un inventario di azioni in alcune società e che avrebbero "fatto un mercato" nelle azioni, intascando il margine tra il loro prezzo di vendita e di acquisto. Ma nel tempo, quando un numero maggiore di partecipanti si è unito al mercato, acquirenti e venditori potrebbero trovarsi più facilmente e la necessità di specialisti e i loro profitti, che equivalevano a una piccola tassa su tutti gli altri, è diminuita. C'è un punto, dice Whitney, in cui un sistema - un mercato o una città - subisce uno spostamento di fase e si riorganizza in modo più efficiente e produttivo.
Whitney, che ha una corporatura leggera e un modo meticoloso, cammina rapidamente attraverso Madison Square Park fino alla Shake Shack, un chiosco di hamburger famoso per il suo cibo e le sue linee. Indica le due finestre di servizio, una per i clienti che possono essere serviti rapidamente, l'altra per gli ordini più complicati. Questa distinzione è supportata da una branca della matematica chiamata teoria delle code, il cui principio fondamentale può essere dichiarato come "il tempo di attesa aggregato più breve per tutti i clienti viene raggiunto quando viene servita per prima la persona con il tempo di attesa più breve previsto, a condizione che il ragazzo che ne desideri quattro gli hamburger con condimenti diversi non impazziscono quando continua a essere inviato sul retro della linea. ”(Questo presuppone che la linea si chiuda in un determinato momento in modo che tutti vengano serviti alla fine. Le equazioni non possono gestire il concetto di infinito aspetta.) L'idea "sembra intuitiva", dice Whitney, "ma doveva essere dimostrata". Nel mondo reale, la teoria delle code viene utilizzata per progettare reti di comunicazione, nel decidere quale pacchetto di dati viene inviato per primo.
Alla stazione della metropolitana di Times Square, Whitney acquista un tariffario, per un importo che ha calcolato per trarre vantaggio dal bonus per il pagamento anticipato e per uscire con un numero pari di corse, senza denaro rimasto inutilizzato. Sulla piattaforma, mentre i passeggeri corrono avanti e indietro tra i treni, parla della matematica della gestione di un sistema di transito. Potresti pensare, dice, che un espresso dovrebbe sempre partire non appena è pronto, ma ci sono momenti in cui ha senso tenerlo nella stazione - per stabilire una connessione con un locale in arrivo. Il calcolo, semplificato, è questo: moltiplicare il numero di persone sul treno espresso per il numero di secondi che verranno tenuti in attesa mentre gira al minimo nella stazione. Ora stima quante persone sul locale in arrivo trasferiranno e moltiplicalo per il tempo medio che risparmieranno portando l'espresso verso la loro destinazione anziché il locale. (Dovrai modellare la distanza percorsa dai passeggeri che si preoccupano di cambiare.) Ciò può portare a potenziali risparmi, in secondi di persona, per il confronto. Il principio è lo stesso a qualsiasi scala, ma è solo al di sopra di una certa dimensione della popolazione che l'investimento in linee della metropolitana a doppio binario o bancarelle di hamburger a due finestre ha un senso. Whitney si imbarca sul locale, dirigendosi in centro verso il museo.
***
Si può anche vedere facilmente che più dati si hanno sull'utilizzo del transito (o ordini di hamburger), più dettagliati e precisi è possibile effettuare questi calcoli. Se Bettencourt e West stanno costruendo una scienza teorica dell'urbanistica, allora Steven Koonin, il primo direttore del Center for Urban Science and Progress della New York University, intende essere in prima linea nell'applicarlo ai problemi del mondo reale. Koonin, a quanto pare, è anche un fisico, un ex professore di Cal Tech e assistente segretario del Dipartimento dell'Energia. Descrive il suo studente ideale, quando CUSP inizia il suo primo anno accademico questo autunno, come "qualcuno che ha aiutato a trovare il bosone di Higgs e ora vuole fare qualcosa con la sua vita che renderà migliore la società". Koonin crede in ciò che a volte viene chiamato Big Data, più grande è, meglio è. Solo nell'ultimo decennio la capacità di raccogliere e analizzare informazioni sul movimento delle persone ha iniziato a raggiungere le dimensioni e la complessità della moderna metropoli stessa. Intorno al periodo in cui ha assunto l'incarico presso il CUSP, Koonin ha letto un articolo sull'afflusso e flusso di popolazione nel quartiere degli affari di Manhattan, basato su un'analisi esaustiva dei dati pubblicati su modelli di occupazione, transito e traffico. È stato un grande lavoro di ricerca, afferma Koonin, ma in futuro non sarà così. "Le persone portano dispositivi di localizzazione nelle loro tasche tutto il giorno", afferma. "Si chiamano cellulari. Non è necessario attendere che un'agenzia pubblichi statistiche di due anni fa. Puoi ottenere questi dati quasi in tempo reale, blocco per blocco, ora per ora.
"Abbiamo acquisito la tecnologia per conoscere praticamente tutto ciò che accade in una società urbana", aggiunge, "quindi la domanda è: come possiamo sfruttare questo per fare del bene? Far funzionare meglio la città, migliorare la sicurezza e promuovere il settore privato? ”Ecco un semplice esempio di ciò che Koonin immagina, nel prossimo futuro. Se, ad esempio, stai decidendo se guidare o prendere la metropolitana da Brooklyn allo Yankee Stadium, puoi consultare un sito Web per i dati di transito in tempo reale e un altro per il traffico. Quindi puoi fare una scelta in base all'intuizione e ai tuoi sentimenti personali sui compromessi tra velocità, economia e convenienza. Questo da solo sarebbe sembrato miracoloso anche qualche anno fa. Ora immagina una singola app che avrebbe accesso a quei dati (oltre alle posizioni GPS dei taxi e degli autobus lungo il percorso, alle telecamere che rilevano i parcheggi dello stadio e ai feed di Twitter da persone bloccate su FDR Drive), considera le tue preferenze e ti informano all'istante: Resta a casa e guarda la partita in TV.
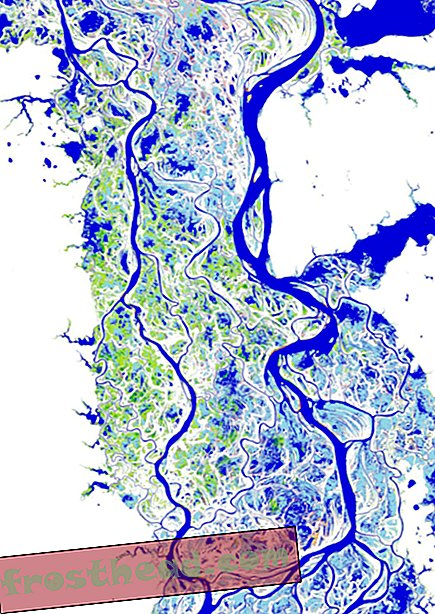
O alcuni esempi leggermente meno semplici di come utilizzare i Big Data. In una conferenza dell'anno scorso Koonin ha presentato l'immagine di una grande fascia di Lower Manhattan, mostrando le finestre di circa 50.000 uffici e appartamenti. È stata scattata con una telecamera a infrarossi e quindi potrebbe essere utilizzata per la sorveglianza ambientale, l'identificazione di edifici o persino singole unità, che perdevano calore e sprecavano energia. Un altro esempio: mentre ti muovi per la città, il tuo cellulare traccia la tua posizione e quella di chiunque entri in contatto. Koonin chiede: Come ti piacerebbe ricevere un sms che ti dice che ieri eri in una stanza con qualcuno che era appena entrato nel pronto soccorso con l'influenza?
***
All'interno del Museo della Matematica, i bambini e gli adulti occasionali manipolano vari solidi su una serie di schermi, ruotandoli, estendendoli o comprimendoli o torcendoli in forme fantastiche, quindi estrudendoli in plastica su una stampante 3D. Si siedono all'interno di un cilindro alto la cui base è una piattaforma rotante e i cui lati sono definiti da stringhe verticali; mentre ruotano la piattaforma, il cilindro si deforma in un iperboloide, una superficie curva che in qualche modo viene creata da linee rette. Oppure dimostrano come sia possibile effettuare una guida fluida su un triciclo a ruote quadrate, se si delinea la pista sottostante per mantenere il livello dell'asse. La geometria, a differenza della logica formale, che era il campo di Whitney prima di andare a Wall Street, si presta particolarmente bene all'esperimento e alla dimostrazione pratica, anche se ci sono anche mostre che toccano campi che identifica come "calcolo, calcolo delle variazioni, equazioni differenziali, combinatoria, teoria dei grafi, ottica matematica, simmetria e teoria dei gruppi, statistica e probabilità, algebra, analisi delle matrici e aritmetica. ”Ha turbato Whitney che in un mondo con musei dedicati a ramen noodles, ventriloquismo, tosaerba e matite, “ la maggior parte di il mondo non ha mai visto la bellezza e l'avventura crude che è il mondo della matematica. ”Questo è ciò che ha deciso di porre rimedio.
Come Whitney sottolinea nei famosi tour di matematica che gestisce, la città ha una geometria distintiva, che può essere descritta come occupando due dimensioni e mezzo. Due di questi sono quelli che vedi sulla mappa. Descrive la mezza dimensione come la rete di passerelle sopraelevate e sotterranee, strade e tunnel a cui è possibile accedere solo in punti specifici, come la High Line, un cavalletto ferroviario abbandonato che è stato trasformato in un parco lineare sopraelevato. Questo spazio è analogo a una scheda elettronica a circuito stampato, in cui, come hanno dimostrato i matematici, alcune configurazioni non possono essere raggiunte su un unico piano. La prova è nel famoso "puzzle a tre utilità", una dimostrazione dell'impossibilità di instradare gas, acqua e servizi elettrici a tre case senza che nessuna delle linee attraversasse. (Puoi vederlo da solo disegnando tre caselle e tre cerchi e provando a connettere ogni cerchio a ciascuna scatola con nove linee che non si intersecano.) In un circuito, affinché i conduttori si incrociano senza toccarsi, a volte uno di loro deve lascia l'aereo. Proprio così, in città, a volte devi salire o scendere per arrivare dove stai andando.
Whitney si dirige verso la città, verso Central Park, dove cammina su un sentiero che per lo più costeggia le colline e le intemperie create dalla glaciazione più recente e migliorate da Olmsted e Vaux. Su una certa classe di superfici continue, di cui un parco è uno, è sempre possibile trovare un percorso che rimanga su un livello. Da vari punti di Midtown, l'Empire State Building appare e scompare dietro le strutture interposte. Questo fa venire in mente una teoria che Whitney ha circa l'altezza dei grattacieli. Ovviamente le grandi città hanno edifici più alti delle piccole città, ma l'altezza dell'edificio più alto in una metropoli non ha un forte rapporto con la sua popolazione; sulla base di un campione di 46 aree metropolitane in tutto il mondo, Whitney ha scoperto che traccia l'economia della regione, approssimando l'equazione H = 134 + 0, 5 (G), dove H è l'altezza dell'edificio più alto in metri e G è il prodotto regionale lordo, in miliardi di dollari. Ma le altezze degli edifici sono vincolate dall'ingegneria, mentre non c'è limite alla quantità di un mucchio che puoi guadagnare con i soldi, quindi ci sono due città molto ricche le cui torri più alte sono più basse di quanto prevedesse la formula. Sono New York e Tokyo. Inoltre, la sua equazione non ha un termine per "orgoglio nazionale", quindi ci sono alcuni valori anomali nell'altra direzione, città la cui portata verso il cielo supera la loro presa di PIL: Dubai, Kuala Lumpur.
Nessuna città esiste nel puro spazio euclideo; la geometria interagisce sempre con la geografia e il clima e con fattori sociali, economici e politici. Nelle metropoli di Sunbelt come Phoenix, a parità di altre condizioni, i sobborghi più desiderabili si trovano ad est del centro città, dove puoi spostarti in entrambe le direzioni con il sole dietro di te mentre guidi. Ma dove c'è un vento prevalente, il posto migliore in cui vivere è (o era, nell'era precedente ai controlli dell'inquinamento) controvento del centro città, che a Londra significa ad ovest. Profondi principi matematici sono alla base anche di fatti apparentemente casuali e storicamente contingenti come la distribuzione delle dimensioni delle città all'interno di un paese. Esiste, in genere, una città più grande, la cui popolazione è doppia rispetto alla seconda più grande, e tre volte la terza più grande, e un numero crescente di città più piccole le cui dimensioni rientrano anche in uno schema prevedibile. Questo principio è noto come la legge di Zipf, che si applica a una vasta gamma di fenomeni. (Tra gli altri fenomeni non correlati, predice come i redditi sono distribuiti in tutta l'economia e la frequenza di comparsa delle parole in un libro.) E la regola è vera anche se le singole città si muovono su e giù nelle classifiche continuamente: St. Louis, Cleveland e Baltimora, tutti nella top 10 di un secolo fa, lasciando il posto a San Diego, Houston e Phoenix.
Come West e i suoi colleghi sono ben consapevoli, questa ricerca si svolge sullo sfondo di un enorme spostamento demografico, il movimento previsto di letteralmente miliardi di persone nelle città dei paesi in via di sviluppo nel corso del prossimo mezzo secolo. Molti di loro finiranno nei bassifondi - una parola che descrive, senza giudizio, insediamenti informali alla periferia delle città, abitati generalmente da occupati abusivi con servizi governativi limitati o assenti. "Nessuno ha fatto un serio studio scientifico su queste comunità", afferma West. “Quante persone vivono in quante strutture di quanti piedi quadrati? Qual è la loro economia? I dati che abbiamo, dai governi, sono spesso senza valore. Nel primo set che abbiamo ricevuto dalla Cina, non hanno riportato omicidi. Quindi lo butti fuori, ma cosa ti rimane? ”
Per rispondere a queste domande, il Santa Fe Institute, con il sostegno della Gates Foundation, ha avviato una partnership con Slum Dwellers International, una rete di organizzazioni comunitarie con sede a Città del Capo, in Sudafrica. Il piano è di analizzare i dati raccolti da 7000 insediamenti in città come Mumbai, Nairobi e Bangalore, e iniziare il lavoro di sviluppo di un modello matematico per questi luoghi, e un percorso per integrarli nell'economia moderna. "Per molto tempo, i responsabili politici hanno ipotizzato che per le città sia una brutta cosa continuare ad allargarsi", afferma Lobo. "Senti cose come" Città del Messico è cresciuta come un cancro ". Un sacco di soldi e sforzi sono stati dedicati a risolverlo, e nel complesso ha fallito miseramente. Città del Messico è più grande di dieci anni fa. Quindi pensiamo che i responsabili politici dovrebbero preoccuparsi invece di rendere quelle città più vivibili. Senza glorificare le condizioni in questi luoghi, pensiamo che siano qui per rimanere e pensiamo che abbiano opportunità per le persone che vivono lì. "
E si sperava meglio che avesse ragione, se Batty ha ragione nel prevedere che entro la fine del secolo, praticamente l'intera popolazione del mondo vivrà in ciò che equivale a "un'entità completamente globale ... in cui sarà impossibile considerare ogni singola città separatamente dai suoi vicini ... anzi forse da qualsiasi altra città. "Stiamo vedendo ora, nelle parole di Bettencourt, " l'ultima grande ondata di urbanizzazione che sperimenteremo sulla Terra ". L'urbanizzazione ha dato al mondo Atene e Parigi, ma anche il caos di Mumbai e la povertà della Londra di Dickens. Se esiste una formula per assicurare che siamo diretti verso l'uno piuttosto che l'altro, West, Koonin, Batty e i loro colleghi sperano di essere quelli che lo troveranno.
